Examining properties of flight

Motion in air is a prime example of how physics and mathematics dominates our lives, exemplifying their synergy. Most physics laws and calculations need complex mathematics to be proven/justified, but mathematics by itself isn't particularly useful in terms of its application in the real world. Thus, this page would mainly show how in-flight motion employs the need to use both physics and mathematics together for better understanding.

Projectile motion

                     

Projectile motion is one of the most common types of movement objects experience in our daily lives, especially in sports that involve a ball. Ranging over tennis, basketball, football, and cricket, projectile motion is certainly at the heart of all of these games. Projectile motion is essentially a 2-dimensional analysis, which may become tricky if one doesn't understand the scenario very well. 

One of the most fundamental properties of projectile motion is the breakdown of the initial velocity vector v into 2 components: vsin(θ) along the y axis and vcos(θ) along the x axis. The simplest yet most commonly confused aspect is that the x axis component vcos(θ) remains unchanged throughout its trajectory since there is no external force acting on it. However, the y component vsin(θ) is subject to the acceleration due to gravity downwards, hence it changes constantly. 

The three main formulae are:

Obviously, these formulae omit the air-resistance, another drag force like friction, but one that opposes motion in air. Although its difficult to quantify, air-resistance will always reduce the three ideal values obtained from the formulae above. Moreover, this assumes that the ball is not spinning during the projectile, as this can cause it to be subject to the Magnus effect.

Air resistance and Terminal Velocity

                                                                                               

 Air resistance is a drag force, where a moving object's surrounding fluid particles that come in contact with the object, oppose its motion. Hence, they always act in the direction opposite of the direction of motion. It is mathematically quantified using the following formula: 

                                                             

For sports like sky-diving, this is an exceptionally important phenomenon, as the skydiver ends up reaching a maximum speed of fall called the terminal velocity. This is the point when the drag force is equal to the weight of the diver. Thus, there is no net force acting causing no change in motion. 

Magnus Effect

The Magnus effect works with the air resistance, altering the simple projectile motion of any object in air. It is a direct consequence of spinning the ball. In the diagram below, the ball is thrown from right to left, hence the air resistance (wind) acts in the opposite side. But since the ball was initially spinning clockwise, there is a change in air pressure above and below the ball. 

                                                               

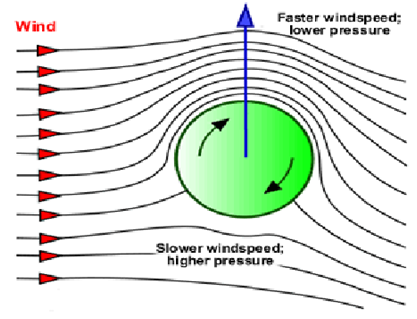
On the upper surface, the ball is turning in the same direction as the wind, causing less friction and low pressure. On the lower surface, its the reverse with more friction and pressure. The different pressures cause a torque which pushes the ball upwards to stay longer in flight.